





















MOLCAS manual: Next: 6.6 MBPT2 A Up: 6. Program Based Tutorials Previous: 6.4 SEWARD An
The simplest ab initio calculations possible use the Hartree-Fock
(HF) Self-Consistent Field (SCF) method with the program name SCF in
the MOLCAS suite. It is possible to calculate the HF energy once we have
calculated the integrals using the SEWARD module, although MOLCAS can perform a direct SCF calculation in which the two-electron integrals are
not stored on disk. The MOLCAS implementation performs a closed-shell (all
electrons are paired in orbitals) and open-shell (Unrestricted Hartree-Fock)
calculation. It is not possible to perform an Restricted Open-shell Hartree-Fock (ROHF)
calculation with the SCF. This is instead done using the program
RASSCF. The SCF program can also be used to perform
calculations using Kohn Sham Density Functional Theory (DFT).
|
 |
&SCF
Title= Water - A Tutorial. The SCF energy of water is calculated using C2v symmetry
End of Input
Irreducible representation : a1
Basis function(s) of irrep: z
Basis Label Type Center Phase
1 O1 1s 1 1
2 O1 2s 1 1
3 O1 2p0 1 1
4 H1 1s 2 1 3 1
Irreducible representation : b1
Basis function(s) of irrep: x, xz, Ry
Basis Label Type Center Phase
5 O1 2p1+ 1 1
6 H1 1s 2 1 3 -1
Irreducible representation : b2
Basis function(s) of irrep: y, yz, Rx
Basis Label Type Center Phase
7 O1 2p1- 1 1
We have ten electrons to ascribe to five orbitals to describe a neutral water molecule in the ground state. Several techniques exist for correct allocation of electrons. As a test of the electron allocation, the energy obtained should be the same with and without symmetry. Water is a simple case, more so when using the minimal basis set. In this case, the fourth irreducible representation is not listed in the GATEWAY output as there are no basis functions in that representation.
To do a UHF calculation, the keyword UHF must be specified. To force a specific occupation for alpha and beta orbitals In this keyword OCCNumbers has to be used with two entries, one for alpha and beta occupied orbital. It is possible to use UHF together with keyword Charge or Aufbau, in this case you have to specify a keyword ZSPIN set to the difference between alpha and beta electrons.
If you want to do an UHF calculation for a closed shell system, for example, diatomic molecule with large interatomic distance, you have to specify keyword SCRAMBLE.
To do the Density Functional Theory calculations, keyword KSDFT followed
in the next line by the name of the available functional as listed in the input
section is compulsory. Presently following Functional Keywords are available:
BLYP, B3LYP, B3LYP5, HFB, HFS, LDA, LDA5, LSDA, LSDA5, SVWN, SVWN5, TLYP, XPBE,
MO6, MO6/HF, MO6/2X, MO6/L.
The description of functional keywords and the functionals is defined in the
section DFT Calculations ![[*]](crossref.png) .
online manual for the SCF program.
.
online manual for the SCF program.
The input for KSDFT is given as,
KSDFT= B3LYP5
In the above example B3LYP5 functional will be used in KSDFT calculations.
6.5.1 Running SCF
Performing the Hartree-Fock calculation introduces some important aspects of the transfer of data between the MOLCAS program modules. The SCF module uses the integral files computed by SEWARD. It produces a orbital file with the symbolic name SCFORB which contains all the MO information. This is then available for use in subsequent MOLCAS modules. The SCF module also adds information to the RUNFILE. Recall that the SEWARD module produces two integral files symbolically linked to ONEINT and ORDINT and actually called, in our case, water.OneInt and water.OrdInt, respectively (this is for non-Cholesky-type calculations only). Because the two integral files are present in the working directory when the SCF module is performed, MOLCAS automatically links them to the symbolic names.
If the integral files were not deleted in a previous calculation the SEWARD calculation need not be repeated. Furthermore, integral files need not be in the working directory if they are linked by the user to their respective symbolic names. Integral files, however, are often very large making it desirable to remove them after the calculation is complete. The linking of files to their symbolic names is useful in other case, such as input orbitals.
If nothing else is stated, the SCF program will use the guess orbitals produced by SEWARD as input orbitals with the internal name GUESSORB. If one wants to use any other input orbitals for the SCF program the option LUMOrb must be used. The corresponding file should be copied to the internal file INPORB. This could for example be an orbital file generated by an earlier SCF calculation, $Project.ScfOrb. Just copy or link the file as INPORB.
6.5.2 SCF Output
The SCF output includes the title from the input as well as the title from the GATEWAY input because we used the integrals generated by SEWARD. The output also contains the cartesian coordinates of the molecule and orbital specifications including the number of frozen, occupied and virtual (secondary) orbitals in each symmetry. This is followed by details regarding the SCF algorithm including convergence criteria and iteration limits. The energy convergence information includes the one-electron, two-electron, and total energies for each iteration. This is followed by the final results including the final energy and molecular orbitals for each symmetry.
The Density Functional Theory Program gives in addition to the above, details of grids used, convergence criteria, and name of the functional used. This is followed by integrated DFT energy which is the functional contribution to the total energy and the total energy including the correlation. This is followed results including the Kohn Sham orbitals for each symmetry.
The molecular orbital (MO) information lists the orbital energy, the electron occupation and the coefficients of the basis functions contributing to that MO. For a minimal basis set, the basis functions correspond directly to the atomic orbitals. Using larger basis sets means that a combination of the basis functions will be used for each atomic orbital and more so for the MOs. The MOs from the first symmetry species are given in Figure 6.5. The first MO has an energy of -20.5611 hartree and an occupation of 2.0. The major contribution is from the first basis function label `O1 1s' meaning an s type function centered on the oxygen atom. The orbital energy and the coefficient indicates that it is the MO based largely on the oxygen 1s atomic orbital.
 |
ORBITAL 1 2 3 4
EneRGY -20.5611 -1.3467 -.5957 .0000
Occ. NO. 2.0000 2.0000 2.0000 .0000
1 O1 1s 1.0000 -.0131 -.0264 -.0797
2 O1 2s .0011 .8608 -.4646 -.7760
3 O1 2p0 .0017 .1392 .7809 -.7749
4 H1 1s -.0009 .2330 .4849 1.5386
The second MO has a major contribution from the second oxygen 1s basis function indicating a mostly oxygen 2s construction. Note that it is the absolute value of the coefficient that determines it importance. The sign is important for determining the orthogonality of its orbitals and whether the atomic orbitals contributions with overlap constructively (bonding) or destructively (anti-bonding). The former occurs in this MO as indicated by the positive sign on the oxygen 2s and the hydrogen 1s orbitals, showing a bonding interaction between them. The latter occurs in the third MO, where the relative sign is reversed.
The third MO has an energy of -0.5957 hartree and major contributions from the second oxygen 1s basis function, the oxygen 2p0 basis function and the hydrogen 1s basis functions which are symmetrically situated on each hydrogen (see Figure 6.4). The mixing of the oxygen 2s and 2p0 basis functions leads to a hybrid orbital that points away from the two hydrogens, to which it is weakly antibonding.
A similar analysis of the fourth orbital reveals that it is the strongly anti-bonding orbital partner to the third MO. The oxygen 2p0 basis function is negative which reverses the overlap characteristics.
The molecular orbital information is followed by a Mulliken charge analysis by input center and basis function. This provides a measure of the electronic charge of each atomic center.
Towards the end of the SCF section of the MOLCAS output various properties of the molecule are displayed. By default the first (dipole) and second cartesian moments and the quadrupoles are displayed.
6.5.3 SCF - Basic and Most Common Keywords
| Keyword | Meaning |
| UHF | Unrestricted Hartee Fock or unrestricted DFT calculation |
| KSDFt | DFT calculations, with options: BLYP, B3LYP, B3LYP5, HFB, HFS, LDA, LDA5, LSDA, LSDA5, SVWN, SVWN5, TLYP, PBE, PBE0 |
| CHARge | Net charge of the system (default zero) |
| ZSPIn | Difference between 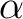 and and 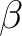 electrons electrons
|
| Occupied | Specify the orbital occupations per irreps |
Next: 6.6 MBPT2 A Up: 6. Program Based Tutorials Previous: 6.4 SEWARD An

