|
MOLCAS manual: Next: 4.7 Analyzing Results: Output Files Up: 4. Quickstart Guide for MOLCAS Previous: 4.5 Input Structure and EMIL
4.6 Basic Examples
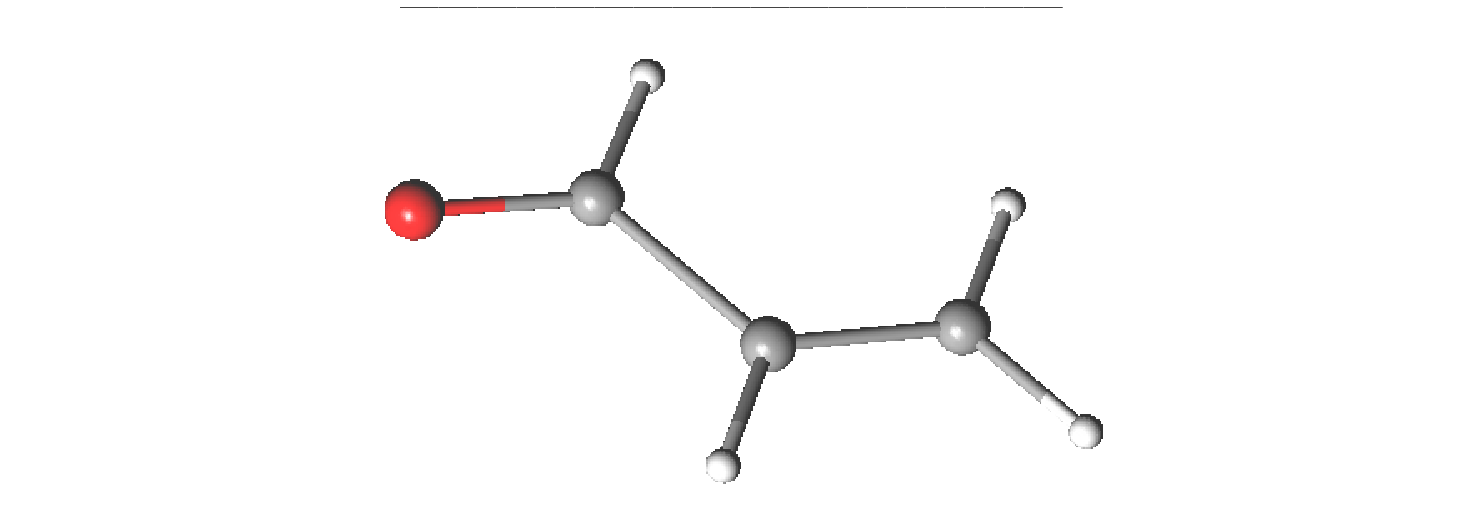
4.6.1 Simple Calculation on WaterStart by preparing a file containing the cartesian coordinates of a water molecule.
which is given the name water.xyz. In the same directory we prepare the input for the MOLCAS run. We can name it water.input: In addition to using an editor to insert atomic coordinates into a file, a coordinate file can be obtained by using a graphical interface program, for example, the LUSCUS module as shown later in this guide.
The GATEWAY program module combines the molecular geometric of water (In this case, from the external file, water.xyz) and the basis set definition. The SEWARD program module then computes the integrals, and SCF program modules completer the calculation by computing the Hartree-Fock wave function. To run the calculation, the following command is used:
The file water.log now contains output from the calculation, and the water.err includes any error messages. In the same directory, other files, including water.scf.molden or water.lus (if the keyword grid_it is added at end of input file) that help to analyze the results graphically with the external graphical viewer LUSCUS or Molden program. Examples of their use are demonstrated below. In the case of an open-shell calculation (UHF or UDFT), the SCF program is again used. Below, two examples are shown:
4.6.2 Geometry OptimizationIn the next example, a DFT/B3LYP geometry optimization is performed on the ground state of the water molecule. Notice that, after &gateway has defined the coordinates and basis set definition, the EMIL commands>>> Do while
and >>> EndDo are employed to form a loop with the
seward, SLAPAF, and SCF programs until convergence of geometry optimization is reached.
Program seward computes the integrals in atomic basis, SCF computes the DFT energy, and the program
SLAPAF controls the geometry optimization and uses the module ALASKA to compute the gradients
of the energy with respect to the degrees of freedom. SLAPAF generates
the new geometry to continue the iterative structure optimization process and
checks to determine convergence parameters are satisfied notifying MOLCAS and stopping the loop.
The above example illustrates the default situation of optimizing to a minimum geometry without any further constraint. If other options are required such as determining a transition state, obtaining a states crossing, or imposing a geometry constraint, specific input should be added to program SLAPAF.
One of the most powerful aspects of MOLCAS is the possibility of computing excited states with multiconfigurational approaches. The next example demonstrates a calculation of the five lowest singlet roots in a State-Average (SA) CASSCF calculation using the RASSCF program. It also illustrates the addition of the CASPT2 program to determine dynamical correlation which provides accurate electronic energies at the CASPT2 level. The resulting wave functions are used in the RASSI module to calculate state-interaction properties such as oscillator strengths and other properties.
Notice that the Group with the option Nosym has been used to prevent GATEWAY from identifying the symmetry of the molecule (Cs in this case). Otherwise, the input of the RASSCF program will have to change to incorporate the classification of the active space into the corresponding symmetry species. Working with symmetry will be skipped at this stage, although its use is very convenient in many cases. A good strategy is to run only GATEWAY and let the program guide you. The RASSCF input describes the active space employed, composed by six active electrons distributed in five active orbitals. By indicating twelve inactive orbitals (always doubly occupied), information about the total number of electrons and the distribution of the orbitals is then complete. Five roots will be obtained in the SA-CASSCF procedurei, and all them will be computed at the CASPT2 level to obtain the transition energies at the higher level of theory. Further, the RASSI will compute the transition properties, in particular, transition dipole moments and oscillator strengths.
4.6.3 GASSCF method
In certain cases it is useful/necessary to enforce restrictions on electronic
excitations within the active space beyond the ones accessible by RASSCF.
These restrictions are meant to remove configurations that contribute only
marginally to the total wave function.
In MOLCAS this is obtained by the GASSCF approach [13].
In GASSCF an arbitrary number of active spaces may be chosen.
All intra-space excitations are allowed (Full-CI in subspaces).
Constraints are imposed by user choice on inter-space excitations.
This method, like RASSCF, allows restrictions on the active space,
but they are more flexible than in RASSCF.
These restrictions are particularly useful when the cost of using the full CI
expansion of the active space is beyond reach.
These restrictions allow GASSCF to be applied to larger and more complex systems
at affordable cost.
Instead of a maximum number of holes in RAS1 and particles in RAS3, accumulated
minimum and maximum numbers of electrons are specified for GAS1, GAS1+GAS2,
GAS1+GAS2+GAS3, etc. in order to define the desired CI expansion.
The GAS scheme reduces to CAS or RAS when one or three spaces are chosen and
restrictions on electron excitations are adequately imposed.
When and how to use the GAS approach?
We consider three examples: (1) an organometallic material with separated metal
centers and orbitals not delocalized across the metal centers. One can include
the near degenerate orbitals of each center in its own GAS space.
This implies that one may choose as many GAS spaces as the number of
multiconfigurational centers. (2) Lanthanide or actinide metal compounds where
the f-electrons require a MC treatment but they do not participate in bonding
neither mix with d orbitals. In this case one can put the f orbitals and their
electrons into one or more separated GAS spaces and not allow excitations
from and/or to other GAS spaces. (3) Molecules where each bond and its correlating
anti-bonding orbital could form a separate GAS space as in GVB approach.
Finally, if a wave function with a fixed number of holes in one or more
orbitals is desired, without interference of configurations where those
orbitals are fully occupied the GAS approach is the method of choice instead
of the RAS approach. There is no rigorous scheme to choose a GAS partitioning.
The right GAS strategy is system-specific. This makes the method versatile but
at the same time it is not a black box method.
An input example follows:
In this example the entire active space counts six active electrons and six active orbitals. These latter are partitioned in three GAS spaces according to symmetry consideration and in the spirit of the GVB strategy. Each subspace has a fixed number of electrons, TWO, and no interspace excitations are allowed. This input shows clearly the difference with the RAS approach.
4.6.4 Solvation EffectsMOLCAS incorporates the effects of the solvent using several models. The most common is the cavity-based reaction-field Polarizable Continuum Model (PCM) which is invoked by adding the keyword RF-input to the SEWARD code and is needed to compute the proper integrals.
The reaction field is computed in a self-consistent manner by the SCF or RASSCF codes and added as a perturbation to the Hamiltonian in the CASPT2 method with the keyword RFPErt.
    
Next: 4.7 Analyzing Results: Output Files Up: 4. Quickstart Guide for MOLCAS Previous: 4.5 Input Structure and EMIL |
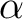than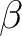 
electrons) states
