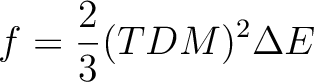




















MOLCAS manual: Next: 10.6 Solvent models. Up: 10. Examples Previous: 10.4 High quality wave functions
The accurate calculation of excited electronic states has been
a challenge for quantum chemistry. The possibility for
accurate calculations of such states in molecules has only
recently been made possible through the development of new
quantum chemical techniques. CASPT2 is currently one of the more
successful methods to compute excited states due to its balance
between accuracy and cost. In addition to the intrinsic
limitations of the method, photochemistry and photophysics
involves a large number of situations and mechanisms which
complicate the problems enormously. In the present section we
are going to show a systematic way to deal with a large
number of states in a molecule. We have selected the thiophene
molecule and our goal will be to compute the lowest valence and
Rydberg singlet states at the ground state geometry. This can
be considered to be the gas-phase absorption spectrum of the molecule.
The calculations comprise an extensive use of the RASSCF,
CASPT2, and RASSI programs. Selection of proper active spaces,
building of appropriate diffuse basis functions, calculation
of transition dipole moments, and use of the level-shift technique
in CASPT2 will be some of the topics covered.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Symmetries | |||||
| a1 | b1 | b2 | a2 | ||
| Frozen orb. | 5 | 1 | 3 | 0 | |
| Inactive orb. | 6 | 0 | 4 | 0 | |
| Valence active orb. | 1 | 3 | 0 | 2 | |
| Rydberg states | ||||||||||
HOMO n=3 n=3 |
State | HOMO-1 n=3 n=3 |
State | HOMO-2 n=3 n=3 |
Statea | |||||
(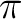 ) a ) a |
3sa1 | A2 | ( ) b ) b |
3sa1 | B1 | (n) a |
3sa1 | A1 | ||
| *[0.2cm] | 3pa1 | A2 | 3pa1 | B1 | ||||||
| 3pb1 | B2 | 3pb1 | A1 | |||||||
| 3pb2 | B1 | 3pb2 | A2 | |||||||
| *[0.2cm] | 3da1 | A2 | 3da1 | B1 | ||||||
| 3da1 | A2 | 3da1 | B1 | |||||||
| 3db1 | B2 | 3db1 | A1 | |||||||
| 3db2 | B1 | 3db2 | A2 | |||||||
| 3da2 | A1 | 3da2 | B2 | |||||||
| Total active space | |
A1, B2 states (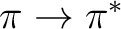 ) ) |
|
1, B2 states (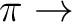 R( R(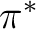 )) )) |
Valence (1302) + Rydberg (0201) = (1503) |
A2, B1 states (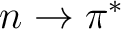 ) ) |
|
A2, B1 states (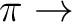 R( R(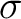 )) )) |
|
| Valence (1302) + Rydberg (4020) = (5322) | |
A1 states (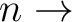 R( R(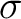 )) )) |
|
| aOnly considered up to the A1 (3s) state because the remaining are expected at higher energy. | |
The computed states will use different partitionings of the active space. The
basic valence space (1302) must be included in all the cases. The valence
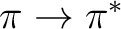 states only involve excitations into the
states only involve excitations into the 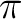 and
and 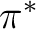 orbitals. Therefore they belong to the A1 and B2 symmetries. In addition
we can have single excitations (Rydberg states) from the occupied
orbitals. Therefore they belong to the A1 and B2 symmetries. In addition
we can have single excitations (Rydberg states) from the occupied 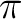 orbitals to the Rydberg orbitals of b1 and a2 symmetries. The number of
Rydberg orbitals belonging to those symmetries is (0201). Thus, the final space
to compute simultaneously valence and Rydberg
orbitals to the Rydberg orbitals of b1 and a2 symmetries. The number of
Rydberg orbitals belonging to those symmetries is (0201). Thus, the final space
to compute simultaneously valence and Rydberg 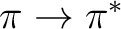 states is
(1302) + (0201): (1503). The same space can be used to compute
states is
(1302) + (0201): (1503). The same space can be used to compute
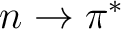 states because the n orbital and the
states because the n orbital and the 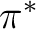 orbitals
are included into the active space. The symmetries of these states, however,
will be A2 and B1. In the table we also have another
division for the A2 and B1,
orbitals
are included into the active space. The symmetries of these states, however,
will be A2 and B1. In the table we also have another
division for the A2 and B1, 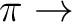 R(
R(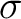 ), and A1,
), and A1, 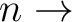 R(
R(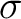 ),
(only the
),
(only the 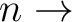 3s) Rydberg states, using an active space (5322).
We have, therefore, divided the excited states to be computed by symmetries
and active space. State-average CASSCF calculations for each one of
the cases have to be performed. The only question which remains is how many roots
we have to include in each of the cases. This is also determined by the symmetry
and active space available. For instance, for the
3s) Rydberg states, using an active space (5322).
We have, therefore, divided the excited states to be computed by symmetries
and active space. State-average CASSCF calculations for each one of
the cases have to be performed. The only question which remains is how many roots
we have to include in each of the cases. This is also determined by the symmetry
and active space available. For instance, for the 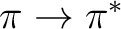 A1 states,
we want to compute the ground state plus three Rydberg states (see Table
A1 states,
we want to compute the ground state plus three Rydberg states (see Table ![[*]](crossref.png) in both
HOMO and HOMO-1
in both
HOMO and HOMO-1  n=3 series) plus a certain number of valence states.
If we do not have any previous experience we may think of three or four possible
valence states but we know that the usual number of low-lying valence
states is close to the number of valence singly excited states, in this case
two of A1 symmetry. This does not mean that the states are
going to be described by one single configuration; it is simply an estimation
of the number of relevant states based on experience. In summary, we expect
to compute six A1 states and therefore we include six roots in the
CASSCF state-average input.
n=3 series) plus a certain number of valence states.
If we do not have any previous experience we may think of three or four possible
valence states but we know that the usual number of low-lying valence
states is close to the number of valence singly excited states, in this case
two of A1 symmetry. This does not mean that the states are
going to be described by one single configuration; it is simply an estimation
of the number of relevant states based on experience. In summary, we expect
to compute six A1 states and therefore we include six roots in the
CASSCF state-average input.
It is not uncommon that one or more valence states do not appear in the initial CASSCF calculation including the desired roots and other higher Rydberg states. This is due to the fact that valence states usually require larger dynamical correlation corrections than the Rydberg states. Therefore in a CASSCF calculation the Rydberg states are, in general, lower in energy than the valence states. The dynamical correlation included by the CASPT2 method will place the states correctly. However this is only possible if the states are present in the CASSCF calculation. It is then necessary to be sure that the states are located at the CASSCF level. Maybe it is necessary to increase the number of roots and in special cases like those with low symmetry even to delete Rydberg orbitals from the active space [25,26,250,260].
In the following we will describe briefly the calculations [261]. A detailed report of the vertical excited spectrum of thiophene can be found in references [261,262]. The selection of the active spaces in that work included additional orbitals to minimize the effect of intruder states. The availability of the level-shift technique in later versions of MOLCAS allow us to use a smaller active space.
10.5.1.2 Generating Rydberg basis functions
First we describe a method for generating Rydberg basis functions for molecules. Such Rydberg orbitals are diffuse and thus require diffuse basis functions. Due to this diffuseness they are not ``localized'' to atoms in the sense that valence orbitals are, but should be considered to be spread out over the entire molecule.
The basis of the method lies in the fact that if we add an electron into a virtual orbital, the energy for the system is increased by the orbital energy, according to Koopmanns' theorem. The reorganizational effects are very minor for the diffuse virtual orbitals. Thus adding an electron into a virtual orbital for a cation is an reasonable approximation to the proper Rydberg state. A more extensive discussion of the method outlined below can be found in [26].
The method can be broken down into a few steps (see Ref. [26] for details):
- Perform a RHF or valence CASSCF calculation of the system with one electron removed, using the RASSCF program. This will determine the center of charge which is a suitable choice to center the Rydberg basis function expansion. The result is rather insensitive to this choice.
- Add a suitable diffuse primitive basis set at the center of charge. We use as universal exponents those optimized by Kaufmann et al. [263] for Rydberg wave functions.
- Repeat the RHF or CASSCF calculation in the new basis.
- Construct the basis set using the program GENANO and use the lowest virtual function to define the basis set.
It is better not to use an extremely large valence basis set to perform these calculations. The best choice is a double-zeta or double-zeta plus polarization basis set. In this example we will use benzene which have a natural origin in the center of the ring. Thus we have eliminated the step of determining the center of charge. Also we have made the simplification of only considering s-functions.
The procedure we will follow is
- Create inputs for SEWARD, SCF, RASSCF, and GENANO.
- Create a shell script to run SEWARD, SCF, and RASSCF, and run the job.
- Hand edit the resulting formated orbital file, C6H6.RasOrb. Set the occupation numbers for the occupied space to zero, while the first three virtual orbitals in the first irreducible representation get the occupation numbers 10-1, 10-2 and 10-3 respectively. These occupation numbers are quite arbitrary as long as they form a decreasing sequence.
- Create a shell script to run GENANO and run the job.
- The resulting file C6H6.Ano now contains the contraction coefficients. Merge this file with the exponents in the SEWARD input to obtain the final contracted basis set. We normally use only one function of each type.
The radial extent of the resulting basis functions is shown in
figure ![[*]](crossref.png) .
.
Here are the inputs used for this example. First the SEWARD input
using the uncontracted Rydberg functions (note that only the s-type Rydberg
basis is shown).
&SEWARD &END
Title
Benzene molecule.
Symmetry
X Y Z
*OneOnly
Basis set
C.ano-s...3s2p1d.
C1 2.636169 .000000 .000000
C2 1.318084 2.282990 .000000
End of basis
Basis set
H.ano-s...2s1p.
H1 4.684633 .000000 .000000
H2 2.342316 4.057011 .000000
End of basis
Basis set
X....8s8p8d. / Inline
0.0 0
8 8
.02462393 .01125334 .00585838 .00334597 .00204842 .00132364 .00089310 .00062431
1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0
X 0.000000 0.000000 .000000
End of basis
End of input
Once computed, the contracted functions will replace the uncontracted ones. In the usual calculations we are going to use one function of each type, 1s1p1d, but we can keep three of them if we want to increase the Rydberg basis for some particular use. Here is the input listing for the generation of the ANO. Note that in newer versions of MOLCAS the sequence of calculations is driven by the input list. You can skip parts of the calculation by commenting out (with a *) the corresponding namelist input ( for example * &SEWARD &END skips the integral calculation).
&SEWARD &END
Title
Benzene molecule.
Symmetry
X Y Z
*OneOnly
Basis set
C.ano-s...3s2p1d.
C1 2.636169 .000000 .000000
C2 1.318084 2.282990 .000000
End of basis
Basis set
H.ano-s...2s1p.
H1 4.684633 .000000 .000000
H2 2.342316 4.057011 .000000
End of basis
Basis set
X....1s1p1d. / Inline
0.0 0
8 1
.02462393 .01125334 .00585838 .00334597 .00204842 .00132364 .00089310 .00062431
.15531366 -.26126804 .38654527
-1.53362747 -1.27182240 .94560891
1.10186802 .95250581 -1.24269525
-1.70918216 .49632170 -2.22724281
2.03031830 .68292933 1.94719179
-1.73187442 -.56245782 .68883478
.92694465 .30675927 .15138171
-.22934028 -.07852136 -.02092438
X 0.000000 0.000000 .000000
End of basis
&SCF &END
Title
Benzene molecule.
Occupied
6 5 4 3 1 1 1 0
End of input
&RASSCF &END
Title
Benzene molecule
Symmetry
7
Spin
2
nActEl
1 0 0
Inactive
6 5 4 3 1 1 0 0
Ras2
0 0 0 0 0 0 1 0
LumOrb
Thrshld
0.5d-8 0.5d-4 1.0d-4
Iterations
50 25
End of input
>>COPY $Project.RasOrb NAT001
>>COPY $Project.OneInt ONE001
>>COPY $Project.RunFile RUN001
&GENANO &END
Title
Rydberg basis set for benzene.
sets
1
Center
X
Weights
1.0
end of input
Here is the shell script used for this example. It is written in Korn shell, but no exotic features of Korn shell are used, so rewriting them into C shell, or whatever your favorite shell is, is a straightforward matter.
#!/bin/ksh
Project='C6H6'
Home=$PWD
WorkDir=/temp1/$LOGNAME/$Project
export Project WorkDir
print 'Start of job:' $Project
print 'Current directory:' $Home
print 'Scratch directory:' $WorkDir
#
trap 'exit' ERR
rm -fr $WorkDir
#
molcas $Home/$Project.input >$Project.output
#
rm -r $WorkDir
For thiophene one can proceed in the same way. The only difference (apart from the fact that we generate s,p,d functions) is that two states of the cation are going to be computed and therefore the final step using the GENANO program will involve two files and have the following input:
!ln -s $Home/Thiophene.Ano ANO
!ln -s $Home/Thiophene.RasOrb1 NAT001
!ln -s $Home/Thiophene.RasOrb2 NAT002
!ln -s Thiophene.OneInt ONE001
!ln -s Thiophene.OneInt ONE002
&GENANO &END
Title
Rydberg basis set for thiophene.
sets
2
Center
X
Weights
0.5 0.5
End of input
The charge centroid is chosen as an average of the charge centroids of the two cations.
10.5.1.3 SEWARD and CASSCF calculations.
Once we have built the diffuse basis set we can proceed with the SEWARD and CASSCF calculations of the different states. Remember that no quantitative result can be expected for calculations which use less than a DZP basis set. Additionally, as we are using methods which include large amounts of correlation, it is also recommended to use basis sets designed to include the correlation, such as the Dunning correlation-consistent basis sets or the Atomic Natural Orbital-type basis sets. Several tests of the accuracy of the ANO-type basis sets for calculations on excited states can be found elsewhere [264]. It was found that the minimum basis set suitable for calculations on excited states is the ANO 3s2p1d basis set for the first row atoms, with 2s functions for the hydrogen. The recommended basis however is an ANO 4s3p1d basis set.
We proceed with the calculations on thiophene. The inputs for the programs SEWARD, SCF, and RASSCF (1A1 states) are:
&SEWARD &END
Title
Thiophene molecule. Experimental gas-phase geometry.
Symmetry
X Y
Basis set
S.ANO-L...5s4p2d.
S1 0.000000 0.000000 0.000000 Bohr
End of basis
Basis set
C.ANO-L...4s3p1d.
C1 0.000000 2.333062 2.246725 Bohr
C2 0.000000 1.344416 4.639431 Bohr
End of basis
Basis set
H.ANO-L...2s1p.
H1 0.000000 4.288992 1.677364 Bohr
H2 0.000000 2.494694 6.327573 Bohr
End of basis
Basis set
X....1s1p1d / Inline
0.0000000 2
* s-type diffuse functions
8 1
.024624 .011253 .005858 .003346 .002048 .001324 .000893 .000624
.38826283
-1.91720062
1.70115553
-2.69265935
3.15654806
-2.69329518
1.44320084
-.35712479
* p-type diffuse functions
8 1
.042335 .019254 .009988 .005689 .003476 .002242 .001511 .001055
.14713386
-.64370136
-.17112583
-.62433766
.58193247
-.53426167
.30777301
-.08250038
* d-type diffuse functions
8 1
.060540 .027446 .014204 .008077 .004927 .003175 .002137 .001491
.24501363
.04635428
.66592833
-.08963981
.52211247
-.32807746
.18219220
-.04616325
X .0000000000 .0000000000 .1609268500
End of Basis
End of Input
&SCF &END
Title
Thiophene molecule
Occupied
11 1 7 3
Iterations
40
End of Input
&RASSCF &END
Title
Thiophene. pipi 1A1 states
Symmetry
1
Spin
1
Nactel
8 0 0
Frozen
4 1 3 0
Inactive
6 0 4 0
Ras2
1 5 0 3
CiRoot
6 6
1 2 3 4 5 6
1 1 1 1 1 1
Iter
50,25
LumOrb
End of Input
>> COPY $Project.JobIph $CurrDir/$Project.1A1.JobIph
*$
The last line will copy the current JOBIPH file to a file in the directory where the job was submitted.
The wave function and natural occupation numbers obtained for the 1A1 states are:
Wave function printout:
occupation of active orbitals, and spin coupling of open shells (u,d: Spin up or down)
~
printout of CI-coefficients larger than 0.38 for root 1
energy= -551.412548
conf/sym 1 22222 444 Coeff Weight
11 2 22000 200 0.95720 0.91624
~
printout of CI-coefficients larger than 0.38 for root 2
energy= -551.192455
conf/sym 1 22222 444 Coeff Weight
14 2 22000 u0d 0.38522 0.14839
20 2 2ud00 200 0.68777 0.47302
~
printout of CI-coefficients larger than 0.38 for root 3
energy= -551.178212
conf/sym 1 22222 444 Coeff Weight
85 2 2u0d0 200 0.74016 0.54783
86 2 2u00d 200 0.46282 0.21421
~
printout of CI-coefficients larger than 0.38 for root 4
energy= -551.155996
conf/sym 1 22222 444 Coeff Weight
12 2 22000 ud0 0.49009 0.24019
14 2 22000 u0d 0.72977 0.53257
~
printout of CI-coefficients larger than 0.38 for root 5
energy= -551.151801
conf/sym 1 22222 444 Coeff Weight
85 2 2u0d0 200 -0.48463 0.23486
86 2 2u00d 200 0.78218 0.61180
~
printout of CI-coefficients larger than 0.38 for root 6
energy= -551.106218
conf/sym 1 22222 444 Coeff Weight
1 2 22200 000 -0.50027 0.25027
20 2 2ud00 200 -0.49511 0.24514
29 2 u2d00 200 0.46904 0.22000
~
Natural orbitals and occupation numbers for root 1
sym 1: 1.999604
sym 2: 1.991918 1.943992 0.097398 0.000219 0.000640
sym 4: 1.904095 0.061524 0.000611
Natural orbitals and occupation numbers for root 2
sym 1: 1.999436
sym 2: 1.947529 1.248261 0.788864 0.028171 0.000731
sym 4: 1.617765 0.032985 0.336259
Natural orbitals and occupation numbers for root 3
sym 1: 1.999273
sym 2: 1.926567 1.085938 0.128802 0.904415 0.000774
sym 4: 1.805386 0.141116 0.007730
Natural orbitals and occupation numbers for root 4
sym 1: 1.999591
sym 2: 1.938931 1.828828 0.185815 0.001667 0.027931
sym 4: 1.100050 0.074750 0.842438
Natural orbitals and occupation numbers for root 5
sym 1: 1.999251
sym 2: 1.935074 1.086440 0.103317 0.001139 0.911640
sym 4: 1.854839 0.074961 0.033340
Natural orbitals and occupation numbers for root 6
sym 1: 1.999766
sym 2: 1.874358 1.484874 1.099307 0.004906 0.008790
sym 4: 1.285113 0.235809 0.007076
We have only included the configurations with weights larger than 10%. Root one corresponds to the closed-shell ground state. To understand the character of the states one must also analyze the orbitals, remembering that the active orbitals are not ordered within the active space.
The following output shows the coefficients of the diffuse functions (center X) which appear in the MOLCAS output. Active orbitals two, three, and six in symmetry 2 are valence orbitals (they have main contributions from the other functions not printed here) and orbitals four and five are Rydberg orbitals. It is usual that they appear as mixed orbitals (3p-3d here) but this mixing has no consequences on the excitation energies. This is also the reason why the Rydberg states appear not as clearly singly configurational states but mixed as in root 5 (see above).
Molecular orbitals for symmetry species 2
~
ORBITAL 2 3 4 5 6
ENERGY .0000 .0000 .0000 .0000 .0000
OCC. NO. 1.8923 1.4570 .4122 .1674 .1689
~
19 X 2px -.0203 .0055 -.0082 .8091 .4535
20 X 3d1+ .0064 -.0037 .0369 .4430 -1.0132
~
Molecular orbitals for symmetry species 4
~
ORBITAL 1 2 3
ENERGY .0000 .0000 .0000
OCC. NO. 1.5865 .1722 .1439
~
15 X 3d2- .0032 .5171 .9600
Both by looking at the configurations and the occupation numbers
we can identify the states. Root two has a main configuration described
by an excitation 3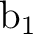
 4
4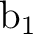 . As 4
. As 4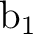 is a valence orbital,
the resulting state will also be a valence state. Root three, on the
contrary, has a main configuration 3
is a valence orbital,
the resulting state will also be a valence state. Root three, on the
contrary, has a main configuration 3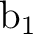
 5
5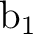 , and 5
, and 5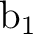 is a
Rydberg orbital. 3
is a
Rydberg orbital. 3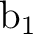 is the HOMO-1 orbital, therefore we can expect the
state represented by root three to be the HOMO-1
is the HOMO-1 orbital, therefore we can expect the
state represented by root three to be the HOMO-1 3px Rydberg
state. So, why does configuration 3
3px Rydberg
state. So, why does configuration 3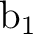
 5
5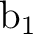 contribute 21% to this
wave function
if a Rydberg state is just a singly excited state?. The answer is in the
composition of the orbitals. Orbitals four and five are a mixture
of px and dxz, and the configurational description must reflect that.
contribute 21% to this
wave function
if a Rydberg state is just a singly excited state?. The answer is in the
composition of the orbitals. Orbitals four and five are a mixture
of px and dxz, and the configurational description must reflect that.
In summary we can make a initial classification of the states:
Root 1: Ground state
Root 2: Valence 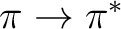 state
state
Root 3: Rydberg 3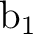
 3px state
3px state
Root 4: Rydberg 3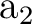
 3dxy state
3dxy state
Root 5: Rydberg 3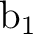
 3dxz state
3dxz state
Root 6: Valence 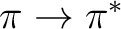 state
state
Orbital two of symmetry 4 also deserves attention. It has large contributions from the diffuse functions, although the remaining non-printed coefficients are even larger. It is an orbital of mixed valence-Rydberg character. This can affect the description of the valence states. In the present system the problem is minor because the orbital does not strongly participate in the description of the valence states as it is shown by the configurations and the occupation numbers, but in other systems the effect is going to be larger as we shall show later.
One important difference between valence and Rydberg states is the diffuse character of the latter. We can analyze the orbital extension of the states. Valence states have an orbital extension (second Cartesian moment) similar to the ground state extension. Rydberg states, on the contrary, should have a diffuse character. Additionally we can also study the Mulliken population analysis. Both appear in the RASSCF output.
Mulliken population Analysis for root number: 1
~
Gross atomic populations per centre and basis function type
~
S1 C1 C2 H1 H2 X
Total 15.8153 12.3470 12.2660 1.6887 1.8021 .0809
~
Expectation values of various properties for root number: 1
~
2-nd Cartesian moments: origin at ( .00000000, .00000000, 2.15947162)
----------------------------------------------------------------------------
Component XX YY ZZ
Total -30.24626427 -21.54920631 -24.73702724
~
Mulliken population Analysis for root number: 2
~
Gross atomic populations per centre and basis function type
~
S1 C1 C2 H1 H2 X
Total 15.6548 12.3730 12.1962 1.6914 1.8015 .2831
Expectation values of various properties for root number: 2
~
2-nd cartesian moments: origin at ( .00000000, .00000000, 2.15947162)
----------------------------------------------------------------------------
Component XX YY ZZ
Total -42.75835009 -28.13902538 -28.72863222
~
Mulliken population Analysis for root number: 4
~
Gross atomic populations per centre and basis function type
~
S1 C1 C2 H1 H2 X
3d2- .0334 .0306 .0413 .0000 .0000 .9662
Total 15.5924 11.8522 12.0083 1.6814 1.7986 1.0671
Expectation values of various properties for root number: 4
~
2-nd cartesian moments: origin at ( .00000000, .00000000, 2.15947162)
----------------------------------------------------------------------------
Component XX YY ZZ
Total -89.85913318 -76.33249740 -44.45493589
~
Mulliken population Analysis for root number: 6
~
Gross atomic populations per centre and basis function type
~
S1 C1 C2 H1 H2 X
Total 15.6154 12.4779 12.3182 1.6946 1.8028 .0911
~
Expectation values of various properties for root number: 6
~
2-nd cartesian moments: origin at ( .00000000, .00000000, 2.15947162)
----------------------------------------------------------------------------
Component XX YY ZZ
Total -31.85163136 -24.13169375 -26.69322385
The Mulliken analysis provides us with the charge distribution per atom and basis function. If we have used for the Rydberg states singly centered Rydberg functions we can observe a population close to one on the X center. This is what happened in root four (see above). In addition we can see that the electron is placed in the 3d2- (3dxy) Rydberg orbital, confirming the character of the state. The orbital extension is undoubtedly much larger in the fourth root than in the ground state. The second and sixth roots however have a much more compact description, especially the sixth, and they have low populations on center X. The second root is somewhat more diffuse but it can be still considered a clear valence state with minor Rydberg mixing.
It is very important to ensure that the relevant states of the symmetry are included in the CASSCF calculation. This may mean performing different experiments by increasing the number of roots and analyzing the results. Valence states are specially sensitive to this because they are high roots at the CASSCF level. Take for instance the sixth root. At the CASSCF level, it is 1.35 eV higher in energy than its preceding root. It could happen that other close Rydberg states or even valence states (such as mainly doubly excited states) were lower at this level of calculation. It can be also helpful to analyze the transition moment to be sure that the intense valence states are present in the set of computed states.
The RASSCF inputs for the remaining states replace the following keywords:
&RASSCF
Title
Thiophene. pipi 1B2 states
Symmetry
3
CiRoot
5 5
1 2 3 4 5
1 1 1 1 1
...
End of Input
>> COPY $Project.JobIph $CurrDir/$Project.1B2.JobIph
*$
&RASSCF
Title
Thiophene. npi 1B1 states
Symmetry
2
CiRoot
1 1
1
...
End of Input
>> COPY $Project.JobIph $CurrDir/$Project.1B1n.JobIph
*$
&RASSCF &END
Title
Thiophene. npi 1A2 states
Symmetry
4
CiRoot
2 2
1 2
1 1
...
End of Input
>> COPY $Project.JobIph $CurrDir/$Project.1A2n.JobIph
*$
&RASSCF &END
Title
Thiophene. pisigma 1B1 states
Symmetry
2
Ras2
5 3 2 2
CiRoot
6 6
1 2 3 4 5 6
1 1 1 1 1 1
...
End of Input
>> COPY $Project.JobIph $CurrDir/$Project.1B1.JobIph
*$
&RASSCF &END
Title
Thiophene. pisigma 1A2 states
Symmetry
4
Ras2
5 3 2 2
CiRoot
6 6
1 2 3 4 5 6
1 1 1 1 1 1
...
End of Input
>> COPY $Project.JobIph $CurrDir/$Project.1A2.JobIph
*$
&RASSCF &END
Title
Thiophene. nsigma 1A1 states
Symmetry
1
Ras2
5 3 2 2
CiRoot
4 4
1 2 3 4
1 1 1 1
...
End of Input
>> COPY $Project.JobIph $CurrDir/$Project.1A1n.JobIph
*$
and use the saved JOBIPH files subsequently.
We must ensure that the right orbitals are included into
the active space. For instance, computing the 1A2 and
1B1 Rydberg states with the active space (5322) we
observe that one Rydberg orbital is absent from the active space
in both cases. For the 1A2 state it was orbital 3dyz.
Instead, an extra-valence 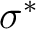 orbital took its place and
therefore the sixth root of symmetry 1A2 was not the expected
2
orbital took its place and
therefore the sixth root of symmetry 1A2 was not the expected
2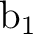
 3dyz Rydberg state. In this case we can reorder
the orbitals including the Rydberg state in the active space
and excluding the other orbital and make the calculation again.
Hopefully the new calculation will include the Rydberg state
into the selected roots. If not we can always increase the
number of roots or increase the active space to have both
orbitals included.
3dyz Rydberg state. In this case we can reorder
the orbitals including the Rydberg state in the active space
and excluding the other orbital and make the calculation again.
Hopefully the new calculation will include the Rydberg state
into the selected roots. If not we can always increase the
number of roots or increase the active space to have both
orbitals included.
It is very important to remember that to compute energy differences one must always use states computed using the same active space. Therefore, if we are computing vertical excitation energies we must have the ground state energy computed in all the different active spaces employed. One can make the comparison using a ground state computed in the average procedure or as a single root. They do not differ significantly. For consistency, we will use a ground state computed as a single root. Therefore we have to perform two CASSCF calculations using the inputs where we replace:
>> COPY $CurrDir/$Project.11A1.JobIph JOBIPH
&RASSCF &END
Title
Thiophene. Ground state (1503)
Symmetry
1
Ras2
1 5 0 3
CiRoot
1 1
1
>> COPY $CurrDir/$Project.11Ar.JobIph JOBIPH
&RASSCF &END
Title
Thiophene. Ground state (5322)
Symmetry
1
Ras2
5 3 2 2
CiRoot
1 1
1
10.5.1.4 CASPT2 calculations.
Once the reference wave functions have been computed at the CASSCF level we can perform the CASPT2 calculations. The JOBIPH file from each CASSCF calculation contains data that describes the state(s). If several CASSCF states are present on a JOBIPH file, then any of this may act as root function for the CASPT2. The input to the CASPT2 must then tell which one of the states we want. In previous MOLCAS version the keyword LROOt was used. Although it will still work, it has been substituted by the more convenient keyword MULTistate, which allows now to perform Multi-State CASPT2 calculations. We will start by discussing single state CASPT2 calculations:
&CASPT2 &END
Title
caspt2 input
MultiState
1 1
End of input
The CASPT2 calculation will be performed on the ground state with the active space (1305), stored on the JOBIPH file that we named $Project.11A1.JobIph. The final full CASPT2 result is:
Reference energy: -551.4423376617
E2 (Non-variational): -.6341237973
E2 (Variational): -.6341237319
Total energy: -552.0764613935
Residual norm: .0000008080
Reference weight: .80657
For a perfectly converged result, the two formulae used to compute E2 are
equivalent, but if there are (as is usually the case) a small residual
error in the CASPT2 equation system, then the variational result is much
more accurate. In particular, for numerical differentiation the variational
energy should always be used. If a level shift has been used, in order to
avoid singularities (see below), then the non-variational energy and the
variational one will differ. The former is the conventional E2 as obtained
with the modified (shifted) 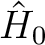 operator, while the latter is a
corrected value very close to what would have been obtained with the unshifted
operator if the near-singular term had been removed. The latter energy is
the one that should normally be used.
operator, while the latter is a
corrected value very close to what would have been obtained with the unshifted
operator if the near-singular term had been removed. The latter energy is
the one that should normally be used.
For the ground state with a reasonable active space, all coefficients in the first order wave function and all contributions to the second-order energy will be small. For excited states, large contributions may occur, and then the second-order perturbation treatment may be invalid. One criterion for a good calculation is that the reference weight should be close to that of the ground state. When this is not true, special remedies may be considered. For example, we compute the CASPT2 correction for the sixth root of symmetry one, using the JOBIPH file called $Project.1A1.JobIph. The input is:
&CASPT2 &END
Title
caspt2 input
MultiState
1 6
End of input
and the result (always full CASPT2 results):
Reference energy: -551.1062184006
E2 (Non-variational): -.7460718503
E2 (Variational): -.7460719607
Total energy: -551.8520232128
Residual norm: .0000009146
Reference weight: .29470
We observe a low weight of 0.295 for the CASSCF reference, compared to the value 0.807 in the ground state. The low weight for the excited state is a warning sign: the second order treatment may be invalid. However, if so, the problem is due to one or a few specific terms in the first-order wave function.
In the output, there is a section with warnings for
large contributions to the energy, low denominator values, or large
coefficients.
~
CASE SYM ACT IND NON-ACT INDICES DENOMINATOR RHS value COEFFICIENT CONTRIBUTION
~
ATVX 2 Mu2.0001 Se2.007 .01778941 -.00706261 .72136097 -.00509469
ATVX 2 Mu2.0001 Se2.009 .20859986 .03118841 -.14372642 -.00448260
ATVX 4 Mu4.0001 Se4.004 .02156184 -.01357269 1.20409651 -.01634282
AIVX 1 Mu1.0001 In1.010 Se1.014 .08105563 .00023689 -.00197645 -.00000047
AIVX 1 Mu1.0001 In3.007 Se3.012 .28275882 -.02231776 .08282960 -.00184857
In CASPT2, the wave operator is a sum of two-electron excitations,
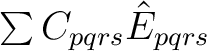 , where the singlet excitation operator
, where the singlet excitation operator
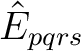 is normal-ordered and summed over spin. The electrons
are transferred from s to r and from q to p.
is normal-ordered and summed over spin. The electrons
are transferred from s to r and from q to p.
No one-electron excitations are used. This is not due to any approximation; it is simply because, for a RASSCF root function with active electrons, the single excitations are exact linear combinations of the double excitations.
The non-orthogonality, as well as the non-diagonal terms of the 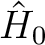 , makes it
difficult (and to some extent irrelevant) to obtain a label that partitions the
wave function and correlation energy in terms of orbital indices of elementary
excitations. However, the CASPT2 program uses internally an orbital system that
diagonalizes part of the Fock matrix: the block diagonal part which does not
include coupling between inactive, active and virtual orbitals. The first-order
wave function, or equivalently the first-order wave operator, can be
subdivided into terms that are grouped into eight different cases. These are named
by four-letter combinations as follows. The letters A, B,C or D are used for
secondary (virtual) orbitals; T, U, V, or X for active ones, and I, J, K or L
for inactive orbitals. A case such as ATVX contains wave operator terms that
can be written as
, makes it
difficult (and to some extent irrelevant) to obtain a label that partitions the
wave function and correlation energy in terms of orbital indices of elementary
excitations. However, the CASPT2 program uses internally an orbital system that
diagonalizes part of the Fock matrix: the block diagonal part which does not
include coupling between inactive, active and virtual orbitals. The first-order
wave function, or equivalently the first-order wave operator, can be
subdivided into terms that are grouped into eight different cases. These are named
by four-letter combinations as follows. The letters A, B,C or D are used for
secondary (virtual) orbitals; T, U, V, or X for active ones, and I, J, K or L
for inactive orbitals. A case such as ATVX contains wave operator terms that
can be written as
 , where a is a virtual orbital and t, v,
and x are active.
, where a is a virtual orbital and t, v,
and x are active.
The first-order wave function can be subdivided into individual terms labeled
by the case (e.g. ATVX), the individual non-active orbital indices, and an
active superindex that labels a linear combination of terms with different
active orbital indices. The linear combination will `mix' all active indices or
index combinations within the case (with symmetry restrictions, if any) in such
a way that the individual terms that are used internally in the CASPT2
programs are orthogonal, and they diagonalize the block-diagonal part of 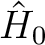 .
.
Of course, the complete 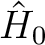 is used to solve the CASPT2 equations, which
is why an iterative procedure is needed. However, in the diagnostic output above,
the "DENOMINATOR" value is that of the resolvent of the block-diagonal part of
is used to solve the CASPT2 equations, which
is why an iterative procedure is needed. However, in the diagnostic output above,
the "DENOMINATOR" value is that of the resolvent of the block-diagonal part of
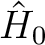 . However, for diagnostics, this is a good approximation. (That it is
not exact only shows by the fact that singularities in the energy do not
occur exactly when the "DENOMINATOR" reported is equal to 0.)
. However, for diagnostics, this is a good approximation. (That it is
not exact only shows by the fact that singularities in the energy do not
occur exactly when the "DENOMINATOR" reported is equal to 0.)
The orbitals are labeled by the symmetry type, a period, and then the ordering number
within that symmetry type. However, for clarity, it also is prefixed by the letters
"Fr", "In", "Ac", "Se" or "De" for frozen (uncorrelated), inactive, active,
secondary, and deleted orbitals. In the wave operator, the only possible orbital
labels are "In" and "Se".
The active superindex is given in formulae as 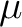 ,
, 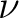 , etc so it is
given a prefix "Mu".
, etc so it is
given a prefix "Mu".
Most of the cases are further subdivided into a plus and a minus linear combination
making altogether 13 cases. Thus, the BVAT case is subdivided into BVATP and BVATM,
containing terms of the type
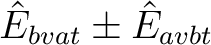 , respectively.
This has nothing to do with spin. It offers some technical advantages in the
equation solution.
, respectively.
This has nothing to do with spin. It offers some technical advantages in the
equation solution.
| Config. | Excitation 1 | Excitation 2 |
| VJTU | Inactive (J)  Active (V) Active (V) |
Active (U)  Active (T) Active (T) |
| VJTIP | Inactive (J)  Active (V) Active (V) |
Inactive (I)  Active (T) Active (T) |
| VJTIM | Inactive (J)  Active (V) Active (V) |
Inactive (I)  Active (T) Active (T) |
| ATVX | Active (T)  Secondary (A) Secondary (A) |
Active (X)  Active (V) Active (V) |
| AIVX | Inactive (I)  Secondary (A) Secondary (A) |
Active (X)  Active (V) Active (V) |
| or: | Active (X)  Secondary (A) Secondary (A) |
Inactive (I)  Active (V) Active (V) |
| VJAIP | Inactive (J)  Active (V) Active (V) |
Inactive (I)  Secondary (A) Secondary (A) |
| VJAIM | Inactive (J)  Active (V) Active (V) |
Inactive (I)  Secondary (A) Secondary (A) |
| BVATP | Active (V)  Secondary (B) Secondary (B) |
Active (T)  Secondary (A) Secondary (A) |
| BVATM | Active (V)  Secondary (B) Secondary (B) |
Active (T)  Secondary (A) Secondary (A) |
| BJATP | Inactive (J)  Secondary (B) Secondary (B) |
Active (T)  Secondary (A) Secondary (A) |
| BJATM | Inactive (J)  Secondary (B) Secondary (B) |
Active (T)  Secondary (A) Secondary (A) |
| BJAIP | Inactive (J)  Secondary (B) Secondary (B) |
Inactive (I)  Secondary (A) Secondary (A) |
| BJAIM | Inactive (J)  Secondary (B) Secondary (B) |
Inactive (I)  Secondary (A) Secondary (A) |
For more details see Refs. [21,22,265]
The first configuration shown in the thiophene output involves the excitation
from the active space to the secondary orbital, which is orbital nr
seven of symmetry two (Se2.007). The denominator value for this
configuration is close to zero (0.01778941). This is an energy difference,
in the 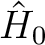 approximation. Thus the root state, and some
eigenstate of
approximation. Thus the root state, and some
eigenstate of 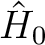 in the interacting space, have almost the same
energy value.
in the interacting space, have almost the same
energy value.
Such states, that were not included in the CASSCF configuration interaction but have energies within the range of the lowest CAS states, cause frequent problems in excited state calculations, since they often give small denominators and even, at particular geometries, singularities. We call these states intruders, by analogy to a similar phenomenon in multi-state perturbation theory. A calculation of excited states by means of a perturbation theory based on an active space has to deal with the problem of intruder states. This is especially common when large and diffuse basis sets, such as the Rydberg functions, are included in the calculations.
In this example, the coefficient to the
first order wave function is large (0.72136094). So is
the contribution to the second order energy (-0.00509469 H),
-0.14 eV. Even worse is the situation for the third term printed
involving the fourth orbital (secondary) of symmetry four
with an energy contribution of 0.44 eV. The analysis of the secondary
orbitals 7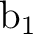 and 4
and 4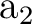 (they are the first virtual orbital of their
symmetry) indicates that they are extremely diffuse orbitals with
large Rydberg character. Remember that the subspaces we are
using are: frozen (4130), inactive (6040), and active (1503).
(they are the first virtual orbital of their
symmetry) indicates that they are extremely diffuse orbitals with
large Rydberg character. Remember that the subspaces we are
using are: frozen (4130), inactive (6040), and active (1503).
This is not the case in the other configurations shown. First we have other ATVX terms including the excitation to the secondary orbital Se2.009. Also we have an AIVX term, involving the excitation from inactive In3.007 to secondary Se3.012. Their contributions to the second order energy, -0.00448260 and -0.00184857, respectively, are not caused by accidental near degeneracies in the value of the denominator. The orbitals involved are not of Rydberg character either. We have finally included as an example the excitation AIVX involving the excitation from In1.010 to Se1.014. Although it has a small value for the denominator, its contribution to the second order energy is very small and therefore it does not represent an important problem.
Intruders can be eliminated by including sufficiently many orbitals in
the active space. When this is a reasonable alternative, it is the preferred
solution. Limitations in the number of active orbitals
can make this approach impractical. However, especially when intruders
have clear Rydberg character, their effect on the second-order energy is
often small, except perhaps in a small range of geometries around a singularity
due to accidental degeneracy. In this common situation, two other remedies
are available: shifting the 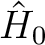 Hamiltonian, or deleting virtual
orbitals. These remedies will be described in some detail in the following.
Hamiltonian, or deleting virtual
orbitals. These remedies will be described in some detail in the following.
In order to obtain continuous potential energy functions, one cannot use a
case-by-case approach, such as deleting an orbital. However, the 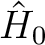 can be modified in such a way as to eliminate weak singularities.
A well-tested method is a level-shift technique called
LS-CASPT2[26,30].
A constant parameter is added to the external part of the zeroth-order
Hamiltonian. Any denominator close to zero is thus shifted away from zero, and
does not produce any singular term. Of course, in a worst-case scenario, it
might happen that some other denominator, previously non-zero, is shifted to
come close to zero. In general,
it is the higher excited states, in combination with large diffuse basis sets
and exploration of a large range of geometries, that is the greatest risk for
troublesome intruders.
can be modified in such a way as to eliminate weak singularities.
A well-tested method is a level-shift technique called
LS-CASPT2[26,30].
A constant parameter is added to the external part of the zeroth-order
Hamiltonian. Any denominator close to zero is thus shifted away from zero, and
does not produce any singular term. Of course, in a worst-case scenario, it
might happen that some other denominator, previously non-zero, is shifted to
come close to zero. In general,
it is the higher excited states, in combination with large diffuse basis sets
and exploration of a large range of geometries, that is the greatest risk for
troublesome intruders.
There is also a new, less tried technique, called the imaginary shift method [32]. Here, the use of an imaginary shift value (but taking the real part of the computed correlation energy) offers some advantage, since an imaginary shift cannot introduce new singularities.
With either of the level shift methods, the (2nd order) correlation energy E2
and the (1st order) wave function will depend on
the level shift used. A correction of therefore applied, whereby in practice
this dependence is made small, except of course for the spurious term that has
disappeared. The corrected energy is in fact computed by using Hylleraas' 2nd-order
variational formula to evaluate E2, with the unshifted 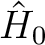 ,
,
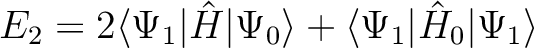 |
(10.3) |
To minimize the effect on relative energies, we recommend that the same level shift is used for all states and geometries, if possible. This may require some experimenting. A criterion on absence of disturbing intruders is that the weight of the reference wave function should be roughly the same in all calculations. Without shift, a difference of up to 10% between the weights of the ground and an excited state can be acceptable (that is, the excitation energy is accurate enough) in a CASPT2 calculation without level shift. Using level shift, this should be adjusted to find a better match of reference weights. A detailed explanation of how to use the level-shift technique has been published [31]. Here we will simply summarize the main aspects.
Using the same JOBIPH file as before we perform a new CASPT2 calculation using the input:
&CASPT2 &END
Title
caspt2 input
MultiState
1 6
Shift
0.1
End of input
A level-shift of 0.1 Hartree has been introduced as a separation of the eigenvalues of the zeroth-order Hamiltonian. The final energy is then corrected, and the result is:
Reference energy: -551.1062184006
E2 (Non-variational): -.6921992859
Shift correction: -.0334372801
E2 (Variational): -.7256365659
Total energy: -551.8315878181
Residual norm: .0000003986
Reference weight: .74942
~
CASE SYM ACT IND NON-ACT INDICES DENOMINATOR RHS value COEFFICIENT CONTRIBUTION
~
ATVX 2 Mu2.0001 Se2.007 .01778941 -.00706261 .06072347 -.00042887
ATVX 2 Mu2.0001 Se2.009 .20859986 .03118841 -.09700134 -.00302532
ATVX 4 Mu4.0001 Se4.004 .02156184 -.01357269 .11838970 -.00160687
AIVX 1 Mu1.0001 In3.007 Se3.012 .28275882 -.02231776 .05918658 -.00132091
Several details come to our attention. Firstly, the final CASPT2 energy is
higher than the result with level-shift 0.0. This is because the introduction
of the parameter decreases the amount of dynamical correlation included.
Secondly, the weight of the reference function has increased greatly, from
0.29 to 0.74, meaning that the most important intruder states have been
removed from the treatment. Finally, we can observe the new contributions
of the printed configurations to the second order energy. Configurations
involving excitations to the 7 and 4
and 4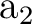 orbitals have drastically decreased
their contributions, proving that the previous contributions
were due to degeneracies in the denominators. However, the other two
configurations remain almost as they were before, only slightly
decreasing their contributions.
orbitals have drastically decreased
their contributions, proving that the previous contributions
were due to degeneracies in the denominators. However, the other two
configurations remain almost as they were before, only slightly
decreasing their contributions.
Now we use a value for the level-shift parameter of 0.2 Hartree:
Reference energy: -551.1062184006
E2 (Non-variational): -.6619040669
Shift correction: -.0557159229
E2 (Variational): -.7176199898
Total energy: -551.8235712419
Residual norm: .0000009298
Reference weight: .78212
~
CASE SYM ACT IND NON-ACT INDICES DENOMINATOR RHS value COEFFICIENT CONTRIBUTION
~
ATVX 2 Mu2.0001 Se2.007 .01778941 -.00706261 .03193515 -.00022555
ATVX 2 Mu2.0001 Se2.009 .20859986 .03118841 -.07304944 -.00227830
ATVX 4 Mu4.0001 Se4.004 .02156184 -.01357269 .06238180 -.00084669
AIVX 1 Mu1.0001 In3.007 Se3.012 .28275882 -.02231776 .04673419 -.00104300
The observed tendencies are maintained. Finally, a value of 0.3 Hartree:
Reference energy: -551.1062184006
E2 (Non-variational): -.6347955450
Shift correction: -.0735679820
E2 (Variational): -.7083635270
Total energy: -551.8145819276
Residual norm: .0000006328
Reference weight: .80307
~
CASE SYM ACT IND NON-ACT INDICES DENOMINATOR RHS value COEFFICIENT CONTRIBUTION
~
ATVX 2 Mu2.0001 Se2.007 .01778941 -.00706261 .02173413 -.00015350
ATVX 2 Mu2.0001 Se2.009 .20859986 .03118841 -.05865340 -.00182931
ATVX 4 Mu4.0001 Se4.004 .02156184 -.01357269 .04240583 -.00057556
AIVX 1 Mu1.0001 In3.007 Se3.012 .28275882 -.02231776 .03862959 -.00086213
The contributions to the energy are much lower for each increase of the parameter, but we must never forget that we are loosing dynamical correlation with the increase of the level-shift factor. In a calculation of excitation energies that means that the resulting excitation energies become larger each time (dynamical correlation is larger in the excited state). Therefore, the level-shift parameter must be set to the lowest possible value which solves the intruder state problems. In practice it is then convenient to scan all the valence states for several values of the parameter and look for two factors:
- Reference weight as close as possible to the ground state reference weight with the same level shift parameter (LS).
- Excitation energies (ES) as stable as possible with the increment of the level-shift parameter (LS).
We now compute the ground state (GS) also for the level-shift values of 0.1, 0.2,
and 0.3, and compare the excitation energies 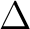 E (always between states
computed with the same parameter):
E (always between states
computed with the same parameter):
| LS (H) | 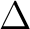 E (eV) E (eV) |
weight GS | weight ES |
| 0.0 | 6.11 | 0.81 | 0.29 |
| 0.1 | 6.64 | 0.82 | 0.75 |
| 0.2 | 6.79 | 0.83 | 0.78 |
| 0.3 | 6.89 | 0.84 | 0.80 |
After checking the remaining states we conclude that a level shift
of 0.1 Hartree is enough for our purposes. However the results
seem to be too unstable with respect to the increase of the level-shift
parameter. As our active space only comprises nine orbitals, we can consider the
possibility of increasing it by including two more active orbitals in
symmetries 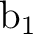 and
and 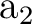 . In this way we minimize the intruder states
problems in the best way, by introducing extra (not diffuse hopefully)
orbitals. This will increase the accuracy.
. In this way we minimize the intruder states
problems in the best way, by introducing extra (not diffuse hopefully)
orbitals. This will increase the accuracy.
The introduction of a (real) level-shift parameter does not automatically remove intruder state problems. It happens that a shift leads to more severe problems that those observed without level-shift. Examples and further explanations are given in e.g. ref. [31]. In such a case is may be possible to find a range of level-shift values where none of the computed states present intruder state problems. In a few cases we have found it necessary to use a shift larger than 0.3 Hartree. Another solution is to try an imaginary shift. This option has not been extensively investigated yet.
Consider a situation like the following:
CASE SYM ACT IND NON-ACT INDICES DENOMINATOR RHS value COEFFICIENT CONTRIBUTION
~
ATVX 2 Mu2.0001 Se2.004 -.30281661 -.00194108 -.37224517 .00072256
This is a calculation performed using level shift of 0.3 H. (The approximate denominator printed in the listing is that without the added shift). We have added the level shift to solve intruder states problem in other states, but we should use the same technique for all the computed states for consistency reasons (of course always using a ground state computed with the same level shift value). We find, however, that the weight of the CASSCF reference function is lower in the case with level shift 0.3 H (0.61) than in the case without level shift (0.69). In this state we have a denominator with a value close to -0.3 H. As the level shift we apply is a positive quantity (0.3 H) added to this denominator, we have created a problem by decreasing the denominator to a value close to zero. The coefficient of the configuration increases, which is reflected in the contributions to the second-order energy. Therefore, before applying any level shift, it is wise to check the values of the most important denominators to see if any of them is going to be close to the value of the applied level shift. In those situations we should set the level shift to another value. Sometimes the consequences for the final energy are small (here for instance) but this is not always the case (see ref. [31]).
It is also possible to delete virtual orbitals. This is occasionally used, e.g. when using other types of basis sets than ANO's, in order to delete virtual orbitals that are core-correlating. The procedure to do that is to take an orbital file, such as that produced by SCF or RASSCF, and edit it by hand and then using it as INPORB file in the RASSCF step. The orbitals one wants to delete are placed at the end of their symmetry group, and the keyword DELEted in used the RASSCF input, indicating how many orbitals are going to be deleted by symmetry. The program will ignore the deleted orbitals, both in RASSCF and the subsequent CASPT2 steps. To obtain accurate energy differences it is necessary to use the same set of initial orbitals and recompute the ground state (or the state one is comparing with) with the same number of deleted orbitals.
When the above scheme is used in order to try to eliminate intruders in CASPT2, the best way is if the INPORB can be prepared from the CASPT2 calculation where the intruder problem occurred.
For that calculation, the natural orbital analysis that follows the CASPT2 calculation shows up a virtual orbital with abnormally large occupation number and diffuse character. Use an editor to move this orbital to the end of the orbital file, and use it as INPORB. When the calculation is repeated, intruders with this orbital heavily populated have been eliminated. Occasionally, several orbitals need to be removed.
The deletion of virtual orbitals works best at single-geometry calculations, such as obtaining the vertical electronic spectrum.
Let us focus on the Multi-State CASPT2 type of calculations. The original reference [15] should be carefully read before using the method. This multidimensional perturbative approach considers the coupling of a number of CASPT2 states, a condition which is crucial to solve certain problems such as adiabatic crossing among states, strong valence-Rydberg situations, etc. The treatment is performed for a number of roots of the same symmetry provided they originate from a previous State-Average CASSCF calculation, that is, the CASPT2 program will use the binary JOBIPH file from a previous SA-CASSCF calculation, for instance, the six roots 1A1 CASSCF calculation in thiophene. The corresponding CASPT2 input to treat simultaneously the six states will be:
&CASPT2 &END
Title
mscaspt2 input
MultiState
6 1 2 3 4 5 6
Shift
0.3
End of input
A level shift parameter of 0.3 au has been selected for comparison with the previous calculations. The program creates a new binary file, JOBMIX, which contains the newly generated Perturbatively Modified (PM) CASSCF wave function.
Using the previous input, the CASPT2 module will perform in a single
run six consecutive single-root CASPT2 calculations for each one of the CASSCF
states. At the end of each of the calculations the contributions to the Hamiltonian
coupling elements between the computed and the remaining states will be printed.
After computing the six CASPT2 roots, the MS-CASPT2 treatment will be performed.
First, the effective Hamiltonian matrix, asymmetric and symmetric, is printed.
Effective Hamiltonian matrix (Symmetric):
1 2 3 4 5
1 -.07013926
2 -.01263691 .12976380
3 .00071175 .01001560 .18051855
4 .00509735 .00990244 -.00321669 .19922802
5 .00607124 .00070650 -.00129815 -.00225583 .21601193
6 .01998132 .02350235 -.00771000 -.01037132 -.00264941
6
1 .18541807
Notice that the diagonal elements of the matrix correspond to the single root CASPT2 state energies, where some quantity, 551.0 au here, has been added to get a better print of the output. Following, the eigenvalues and eigenvectors of the diagonalized matrix are obtained:
Energies and eigenvectors:
-552.07305076 -551.88140802 -551.81866833 -551.80756578 -551.79500203
.99308520 -.10131857 .01038991 .05207094 -.02055799
.07343489 .90295279 .31190606 .28061095 -.05245262
-.00869768 -.19493901 .90626880 -.37241673 .03796203
-.02478279 -.15572120 .13596794 .50373403 .83205915
-.02204833 -.01553573 .05330075 .08679334 .05789830
-.08492920 -.33454317 .24485766 .72011863 -.54745806
-551.78350398
.01655899
-.02245882
-.02155609
-.10285444
.99274682
-.05129770
The eigenvalues correspond to the final MS-CASPT2 energies, while the eigenvectors describe the combination of the coupled CASPT2 state which give rise to the final MS-CASPT2 states. Important: Notice that the states are written in an increasing energy order, and therefore they do not, in general, correspond to the order obtained in the previous SA-CASSCF calculation. For instance, the MS-CASPT2 state number six, energy -551.78350398 au, mainly correspond to the fifth state of the previous calculation. It is very important to remember that the final states are linear combinations of the preceding ones, and therefore a one to one correspondence is hardly possible. In the present example most of the MS-CASPT2 states have a strong weight in just one of the preceding states, but this is not the case in many situations. Following in the output, a printing of the new wave function is obtained. It corresponds to linear combinations of the SA-CASSCF CI wave functions, obtained in the basis of the previous CASSCF averaged orbitals.
The CI coefficients for the MIXED state nr. 1
----------------------------------------------------------------------------
CI COEFFICIENTS LARGER THAN 0.36
Occupation of active orbitals, and spin coupling
of open shells. (u,d: Spin up or down).
Conf Occupation Coef Weight
11 2 22000 200 .960835 .923204
The CI coefficients for the MIXED state nr. 2
----------------------------------------------------------------------------
CI COEFFICIENTS LARGER THAN 0.36
Occupation of active orbitals, and spin coupling
of open shells. (u,d: Spin up or down).
Conf Occupation Coef Weight
20 2 2ud00 200 .856751 .734023
The CI coefficients for the MIXED state nr. 3
----------------------------------------------------------------------------
CI COEFFICIENTS LARGER THAN 0.36
Occupation of active orbitals, and spin coupling
of open shells. (u,d: Spin up or down).
Conf Occupation Coef Weight
85 2 2u0d0 200 .764848 .584993
86 2 2u00d 200 .507350 .257404
The CI coefficients for the MIXED state nr. 4
----------------------------------------------------------------------------
CI COEFFICIENTS LARGER THAN 0.36
Occupation of active orbitals, and spin coupling
of open shells. (u,d: Spin up or down).
Conf Occupation Coef Weight
1 2 22200 000 -.368003 .135427
14 2 22000 u0d .732276 .536229
The CI coefficients for the MIXED state nr. 5
----------------------------------------------------------------------------
CI COEFFICIENTS LARGER THAN 0.36
Occupation of active orbitals, and spin coupling
of open shells. (u,d: Spin up or down).
Conf Occupation Coef Weight
1 2 22200 000 .416925 .173826
12 2 22000 ud0 .549793 .302272
14 2 22000 u0d .455052 .207072
The CI coefficients for the MIXED state nr. 6
----------------------------------------------------------------------------
CI COEFFICIENTS LARGER THAN 0.36
Occupation of active orbitals, and spin coupling
of open shells. (u,d: Spin up or down).
Conf Occupation Coef Weight
85 2 2u0d0 200 -.517972 .268295
86 2 2u00d 200 .776117 .602358
The comparison of the present wave functions, that will be hereafter
called Perturbatively Modified (PM) CASSCF wave functions, and the
previous CASSCF wave functions leads to several conclusions. Remember
that the orbital basis has not changed, therefore those mixing related
to the orbitals are not going to disappear. For instance, state number
three will still be formed by two configurations, because the Rydberg
3px character is still delocalized between orbitals 5 and 6 or symmetry
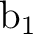 . However the character of the second root has changed dramatically.
Now one single configuration describes the state, which has acquired a
very clear valence character. The previous mixing with a Rydberg-like
configuration has disappeared. It is illustrative to carry out
an additional analysis of the obtained states using the generated
file JOBMIX as input file to perform
a RASSI calculation, in which new PM-CASSCF properties
for the states will be obtained. Even when the changes in energies
are small, changes in the properties can be considerable.
RASSI provides different types of matrix elements
(see next section), and dipole moments, transition dipole moments
and their directions, and orbital extensions (all of them available
from the RASSI output) will be crucial for our purposes
in the study of excited states.
. However the character of the second root has changed dramatically.
Now one single configuration describes the state, which has acquired a
very clear valence character. The previous mixing with a Rydberg-like
configuration has disappeared. It is illustrative to carry out
an additional analysis of the obtained states using the generated
file JOBMIX as input file to perform
a RASSI calculation, in which new PM-CASSCF properties
for the states will be obtained. Even when the changes in energies
are small, changes in the properties can be considerable.
RASSI provides different types of matrix elements
(see next section), and dipole moments, transition dipole moments
and their directions, and orbital extensions (all of them available
from the RASSI output) will be crucial for our purposes
in the study of excited states.
Finally, it is necessary to remember that the extent of the MS interaction relies on the mixing of the previous states. This depends on different factors. The basis sets is one of them. The use of one or other atomic basis set to describe the diffuse functions may lead to different answers. It is not uncommon that CASPT2 results with different diffuse basis sets give different answers due to different extents of the valence-Rydberg mixing. It will be necessary to perform final MS-CASPT2 calculations. Those will change the CASPT2 result in some cases, but it will be unaffected in other cases. Another effect comes from the use of the level shift. The use of MS-CASPT2 does not prevent or affect the extent of the intruder effects. Remember that this effect is already included both in the diagonal terms of the effective Hamiltonian as in the non-diagonal coupling terms. Still a careful checking of different LS values and how they affect the CASPT2 values must be performed, and the final MS-CASPT2 results should be those in which the effect of the intruder states is small, always trying to use as low level shift values as possible. An alternative is to use an imaginary level shift. Finally, the extent of the off-diagonal coupling elements and its asymmetric character introduce further inaccuracies in the treatment. In most cases the proper enlargement of the active space diminishes most of the spurious effects and increases the accuracy.
10.5.1.5 Transition dipole moment calculations.
One powerful tool included in the MOLCAS package is the RASSI program. RASSI (RAS State Interaction) forms matrix elements of the Hamiltonian and other operators in a wave function basis which consists of individually optimized CI expansions from the RASSCF program. It also solves the Schrödinger equation within the space of these wave functions. In spectroscopy we need to compute the matrix elements of a one-electron operator such as the dipole transition moment to obtain the intensity of the transitions. In an absorption process this means computing the interaction of the ground state with the excited states. RASSI will compute all matrix elements among the states provided they have been computed with the number of inactive and active orbitals, and using the same basis set. The transition dipole moments are computed using the length representation.
In our example we have used two different active spaces.
We therefore need to perform at least two RASSI calculations.
First we will compute the interaction of the ground
state 11A1 (computed as single root), with the 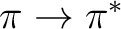 1A1 and 1B2 excited states. We should link the corresponding
JOBIPH files:
1A1 and 1B2 excited states. We should link the corresponding
JOBIPH files:
ln -fs $Project.11A1.JobIph JOB001
ln -fs $Project.1A1.JobIph JOB002
ln -fs $Project.1B2.JobIph JOB003
and use the RASSI input file:
&RASSI &END
Nrofjobiphs
3 1 5 5
1
2 3 4 5 6
1 2 3 4 5
End of input
As we are using states that are not orthogonal (this is the case among the 11A1 ground state computed as a single root and the other 1A1 states) we must take the matrix elements of the transition dipole moment computed after the transformation to the eigenbasis; the second time they appear in the output:
PROPERTY: MLTPL 1 COMPONENT: 2
ORIGIN : .00000000D+00 .00000000D+00 .00000000D+00
STATE : 1 2 3 4
~
1 .00000000D+00 .00000000D+00 -.43587844D+00 .00000000D+00
2 .00000000D+00 .00000000D+00 -.10019699D+01 .00000000D+00
3 -.43587844D+00 -.10019699D+01 .00000000D+00 -.46859879D+00
4 .00000000D+00 .00000000D+00 -.46859879D+00 .00000000D+00
5 .90773544D-01 .75718497D-01 .00000000D+00 .27645327D+00
6 .00000000D+00 .00000000D+00 .41227462D+01 .00000000D+00
7 .00000000D+00 .00000000D+00 .89741299D+00 .00000000D+00
8 -.16935368D+00 .15487793D+01 .00000000D+00 -.41013917D+01
9 .81381108D+00 .79559359D+00 .00000000D+00 -.88184724D-01
10 .00000000D+00 .00000000D+00 -.43659784D+00 .00000000D+00
11 .13520301D+01 .50454715D+00 .00000000D+00 .56986607D-01
~
...
~
PROPERTY: MLTPL 1 COMPONENT: 3
ORIGIN : .00000000D+00 .00000000D+00 .22419033D+01
STATE : 1 2 3 4
1 .28126942D+00 -.92709234D+00 .00000000D+00 .11876829D+00
2 -.92709234D+00 .26218513D+00 .00000000D+00 .14100968D+00
3 .00000000D+00 .00000000D+00 .52558493D-01 .00000000D+00
4 .11876829D+00 .14100968D+00 .00000000D+00 .36996295D+00
5 .00000000D+00 .00000000D+00 -.43197968D+01 .00000000D+00
6 -.15470487D+00 -.42660550D+00 .00000000D+00 .94593876D+00
7 -.18676753D-01 .18738780D+01 .00000000D+00 -.37737952D+01
8 .00000000D+00 .00000000D+00 -.28182178D+00 .00000000D+00
9 .00000000D+00 .00000000D+00 .38253559D+00 .00000000D+00
10 .12859613D+01 .48476356D+00 .00000000D+00 .35525361D+00
11 .00000000D+00 .00000000D+00 -.39325294D-01 .00000000D+00
We have a symmetric matrix containing the results. The matrix elements
corresponding to the interaction of the first state in the input
(ground state) and the remaining states appear both in the first
column and in the first row (only partially printed here). Remember
that the transition dipole moment (TDM) matrix elements are determined by the symmetry.
The matrix element
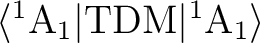 will be zero for the
x and y components of TDM, and non-zero otherwise.
The matrix element
will be zero for the
x and y components of TDM, and non-zero otherwise.
The matrix element
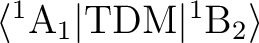 will be non-zero only
for the y component of TDM. This is because the product
(wave function 1 x dipole moment component x wave function 2), if decomposed into
irreducible representations, must contain the
totally symmetric representation to have an allowed transition. In this simple case,
we can use a multiplication table for the irreps.
Thus, for instance, ( 1A1 (z) x TDMy x 1A1 (z) ) gives y, which
does not belong to the totally symmetric representation. A look at the
character table and the behavior of the x,y,z functions will give us the
information we need.
will be non-zero only
for the y component of TDM. This is because the product
(wave function 1 x dipole moment component x wave function 2), if decomposed into
irreducible representations, must contain the
totally symmetric representation to have an allowed transition. In this simple case,
we can use a multiplication table for the irreps.
Thus, for instance, ( 1A1 (z) x TDMy x 1A1 (z) ) gives y, which
does not belong to the totally symmetric representation. A look at the
character table and the behavior of the x,y,z functions will give us the
information we need.
Therefore, in the component two (y) of the transition dipole moment matrix elements we have zero values for the interaction among 1A1 states and non-zero values for the interaction among 1A1 and 1B2 states.
The RASSI program in 6.0 and later versions of MOLCAS will print the oscillator strengths and the Einstein A coefficients for all transitions. Also the angles of the transition moment vectors to the coordinate axes will be printed. In the calculation RASSI will use the energies given as input, so be careful to use the keywords HDIAG or EJOB to use energies which include dynamic correlation.
We illustrate how the oscillator strengths are computed. The 11 states are ordered by CASSCF energies. We focus on the valence states; firstly the fourth and fifth 1B2 states. Their transition dipole moment values in atomic units are 0.81381108 and 0.13520301D+01, respectively. The oscillator strength is defined as:
The energy difference 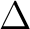 E is the excitation energy expressed in atomic
units. The transition moments were computed by CASSCF. It is usually not practically
possible to compute them with dynamic correlation included, except if a common set
of orbitals are used. However, the CASSCF values are usually good enough.
(Exceptions occur, e.g. close to narrowly avoided crossings or conical intersections).
The excitation energies, on the other hand, are quite sensitive to dynamic
correlation.
Thus, it is a good approach to
use CASSCF TDMs and CASPT2 excitation energies. The values for the oscillator
strengths of the two 1B2 valence states are 0.086 and 0.324, respectively.
The excitation energies are 5.31 and 7.23 eV, respectively. All data corresponds
to results obtained using the 0.1 Hartree value for the level-shift parameter.
E is the excitation energy expressed in atomic
units. The transition moments were computed by CASSCF. It is usually not practically
possible to compute them with dynamic correlation included, except if a common set
of orbitals are used. However, the CASSCF values are usually good enough.
(Exceptions occur, e.g. close to narrowly avoided crossings or conical intersections).
The excitation energies, on the other hand, are quite sensitive to dynamic
correlation.
Thus, it is a good approach to
use CASSCF TDMs and CASPT2 excitation energies. The values for the oscillator
strengths of the two 1B2 valence states are 0.086 and 0.324, respectively.
The excitation energies are 5.31 and 7.23 eV, respectively. All data corresponds
to results obtained using the 0.1 Hartree value for the level-shift parameter.
Remember that in other symmetries like C2h the 1B2 states have two components of TDM, x and y, for which the matrix elements with respect to the ground state are non-zero. In this case the TDM2 value is computed as TDMx2 + TMDy2. In those cases is is also possible to compute the direction of the total TDM vector by taking their components and compute the angle respect to any of the axis.
You will find the complete calculation of the absorption spectrum of thiophene in reference [249]. You can observe that, despite there being no level-shift technique used, the final results on the excitation energies agree to within 0.1 eV to those shown here.
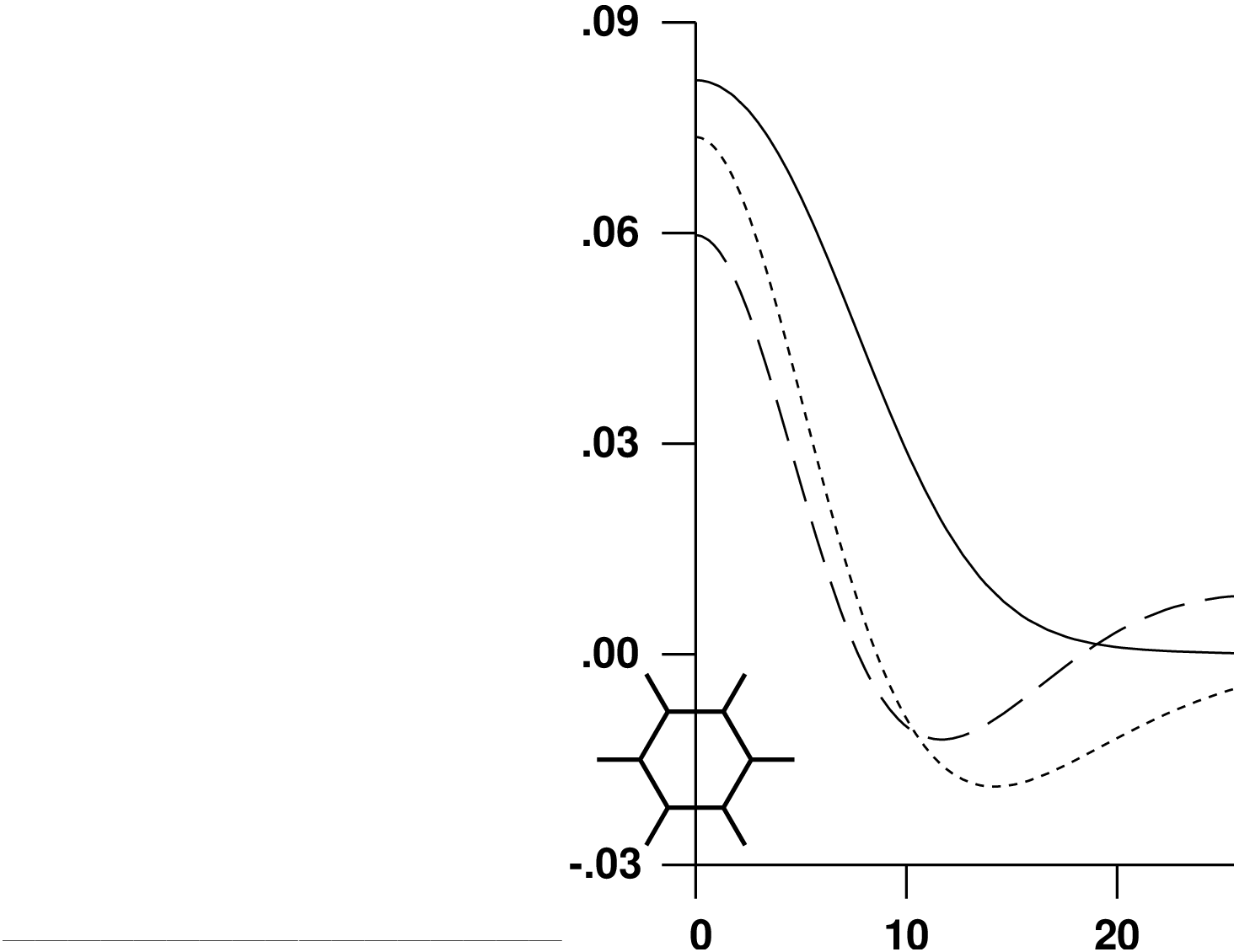
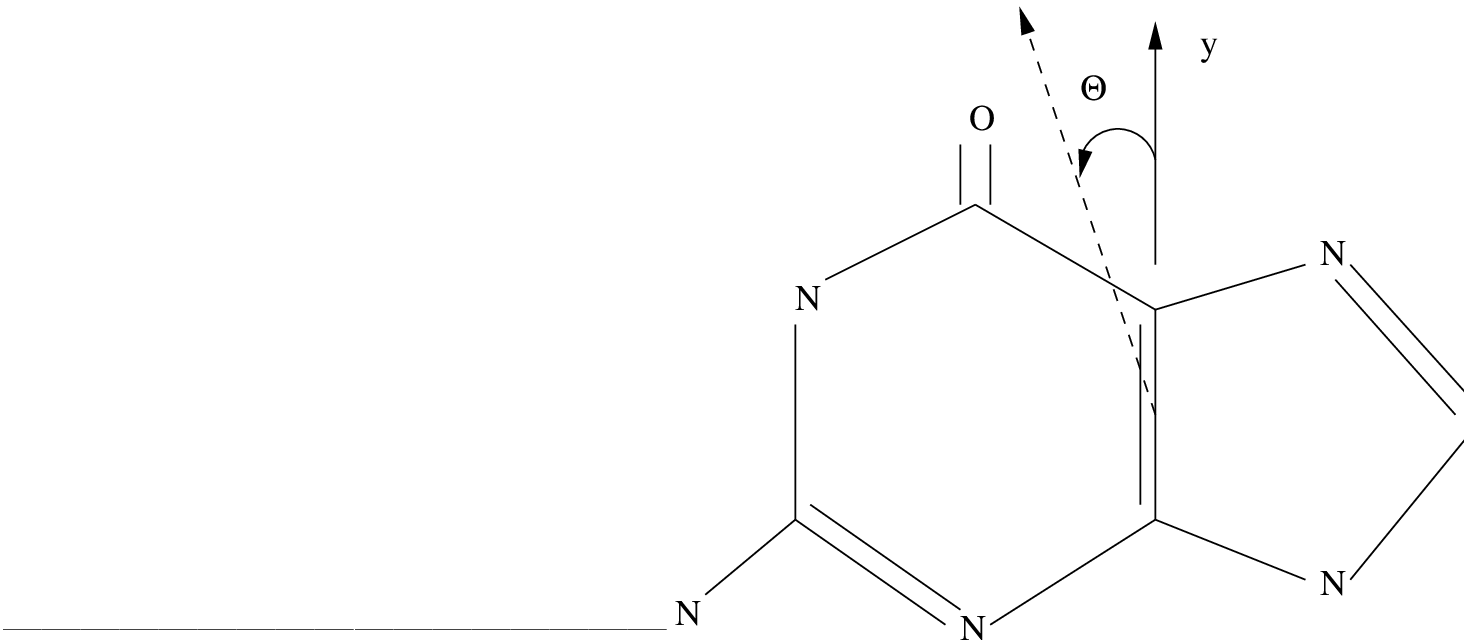
10.5.2 Influence of the Rydberg orbitals and states. One example: guanine.
Thiophene has a valence 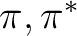 orbital space small
enough to allow the simultaneous inclusion of all the corresponding Rydberg orbitals
into the active space (remember valence space (1302) + Rydberg spaces
(0201) or (4020)), but this is not always the case. In addition, the
valence-Rydberg mixing is not severe. This mixing is reflected
in the orbital extension or the population analysis. In difficult cases
valence and Rydberg orbitals mix, and then the configurations also mix.
Valence states become more diffuse and Rydberg states more compact.
Energetically this has minor consequences for the Rydberg states, which
can be computed using these CASSCF mixed wave functions. This is not
the case for the valence states. They are extremely sensitive to the
mixing. Therefore, if we do not observe clear and compact valence states
some mixing has occurred.
orbital space small
enough to allow the simultaneous inclusion of all the corresponding Rydberg orbitals
into the active space (remember valence space (1302) + Rydberg spaces
(0201) or (4020)), but this is not always the case. In addition, the
valence-Rydberg mixing is not severe. This mixing is reflected
in the orbital extension or the population analysis. In difficult cases
valence and Rydberg orbitals mix, and then the configurations also mix.
Valence states become more diffuse and Rydberg states more compact.
Energetically this has minor consequences for the Rydberg states, which
can be computed using these CASSCF mixed wave functions. This is not
the case for the valence states. They are extremely sensitive to the
mixing. Therefore, if we do not observe clear and compact valence states
some mixing has occurred.
We consider
the example of the guanine molecule, the nucleic acid base monomer.
It is a system with 11 valence 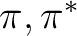 orbitals which should be included
into the active space. It is a planar system
in the Cs point group. Focusing only in the
orbitals which should be included
into the active space. It is a planar system
in the Cs point group. Focusing only in the 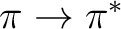 states
we can label the active orbital space (0,11) where 0 is the number of
a' orbitals and 11 the number of a'' orbitals. In Cs symmetry the
Rydberg orbitals are distributed as (6,3), using the same labeling.
Therefore the calculation of the corresponding A' states should
use the space (0,14) with 14 active electrons and a large number of
roots. This is a large calculation that one might want to avoid.
One can perform several
test calculations (maybe even RASSCF calculations) and find if
any orbitals can be excluded. The lowest occupied
states
we can label the active orbital space (0,11) where 0 is the number of
a' orbitals and 11 the number of a'' orbitals. In Cs symmetry the
Rydberg orbitals are distributed as (6,3), using the same labeling.
Therefore the calculation of the corresponding A' states should
use the space (0,14) with 14 active electrons and a large number of
roots. This is a large calculation that one might want to avoid.
One can perform several
test calculations (maybe even RASSCF calculations) and find if
any orbitals can be excluded. The lowest occupied
 orbital is a deep orbital which does not participate in the
lowest valence excited states and can be excluded from the active
space. Despite this exclusion, a (0,13) orbitals calculation is
still expensive. We can proceed in another way.
Consider the new valence space (0,10), and add only one more
orbital designed to include the first Rydberg orbital.
With this space of (0,11) orbitals and 12 active electrons we perform
a CASSCF including 6 roots.
orbital is a deep orbital which does not participate in the
lowest valence excited states and can be excluded from the active
space. Despite this exclusion, a (0,13) orbitals calculation is
still expensive. We can proceed in another way.
Consider the new valence space (0,10), and add only one more
orbital designed to include the first Rydberg orbital.
With this space of (0,11) orbitals and 12 active electrons we perform
a CASSCF including 6 roots.
Our basis set is of the ANO-L type
contracted to C,N,O 4s3p1d / H 2s, plus 1s1p1d optimized
diffuse functions placed in the cation charge centroid.
The results are collected in Table ![[*]](crossref.png) .
.
| State | Theoretical | Experimentb | |||||||
| CAS | PT2 | f |  |
 |
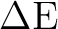 |
f | 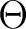 |
||
 – – transitions transitions |
|||||||||
| 21A' | 5.72 | 4.47 | .20 | -64o | 1.07 | 4.4-4.5 | .16 | (-4o,35o) | |
| 31A' | 6.74 | 5.30 | .09 | +52o | 2.72 | 4.9-5.0 | .25 | (-75o) | |
| 41A' | 7.18 | 5.63 | .05 | -90o | 3.10 | 5.7-5.8 | <.05c | ||
| 51A' | 8.45 | 6.83 | .26 | 0o | 3.20 | 6.1-6.3 | .41 | (-71o,-79o) | |
| aSee ref. [266] for details. | |||||||||
There are important discrepancies between theoretical and experimental results, more important in the properties such as the intensities and the transition dipole moments than in the excitation energies. If we analyze the CASSCF output everything is apparently correct: six converged roots, all of them clear valence states, and no Rydberg orbital into the active space. This is the problem. At least one of the Rydberg orbitals should have been introduced into the active space. Rydberg and valence orbitals must be treated simultaneously and this is not possible if there is no Rydberg orbital in the active space.
The correct way to proceed is to take the first Rydberg orbital (3pz) and place it as the 11th active orbital of a'' symmetry. Then the CASSCF calculation will retain it in the space. Once the calculation has converged we observe than at least one of the computed states is of Rydberg character. It can also happen that some mixing appears in the valence states due to the presence of the diffuse orbital in the active space. The Rydberg orbital is then removed (placed in the last position of its symmetry and the DELEte option used) from the active space and the calculation repeated. This time the next Rydberg orbital (3dxz or 3dyz) will take its place. The process is repeated once again until the three Rydberg orbitals have been first included in the active space and then deleted (option DELEted of the RASSCF program). Now we can reduce the active space to (0,10), only including valence orbitals and valence excited states.
We can repeat the calculation including even more roots. The results
are in Table ![[*]](crossref.png) .
.
 =0pt
=0pt
=0pt
=0pt
| State | Theoretical | Experiment | ||||||||
| CAS | PT2 | f | 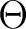 |
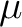 |
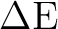 |
f | 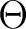 |
|||
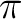 – –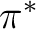 transitions transitions |
||||||||||
| 21A' | 6.08 | 4.76 | .133 | -15o | 7.72 | 4.4-4.5 | .16 | (-4o,35o) | ||
| 31A' | 6.99 | 5.09 | .231 | +73o | 6.03 | 4.9-5.0 | .25 | (-75o) | ||
| 41A' | 7.89 | 5.96 | .023 | +7o | 5.54 | 5.7-5.8 | <.05c | |||
| 51A' | 8.60 | 6.65 | .161 | -80o | 10.17 | 6.1-6.3 | .41 | (-71o,-79o) | ||
| 61A' | 9.76 | 6.55 | .225 | -41o | 6.11 | |||||
| 71A' | 8.69 | 6.66 | .479 | +43o | 6.57 | 6.6-6.7 | .48 | (-9o,41o) | ||
| 81A' | 9.43 | 6.77 | .098 | +52o | 7.17 | |||||
| aSee ref. [266] for details. | ||||||||||
| bA better match with the experimental values is obtained by considering solvent effects. | ||||||||||
The results are quite different from those obtained previously, especially regarding the oscillator strengths and transition dipole moment directions. What we have before was a set of states with valence-Rydberg character, although it was not reflected in the orbital extension or population analysis because the orbitals in the active space were too compact to be able to reflect it. The states we have now are also of clear valence character but the difference is that we have first included the Rydberg orbitals in the active space, allowed the flexibility to describe the Rydberg state, and then removed them from the space to finish with a set of compact valence orbitals which cannot represent the Rydberg states. Then, the latter are removed from the computed spectrum of states.
The experience of this type of treatment in different molecules [26,30,266] points out that if the valence states of a molecule are computed without considering the Rydberg states and functions (whether by excluding them from the basis set or from the active space) can result in an additional CASPT2 error as large as 0.3-0.4 eV. The errors are more severe for other transitions properties. One example of this can be found for two different CASPT2 treatments of the formamide molecule, one including diffuse functions and other excluding them (see ref. [267] for details). Notice, however, that this approach cannot describe a true valence-Rydberg mixing. An alternative to such an approach is to use the Multi-State CASPT2 treatment that, although computationally expensive, might properly treats the valence-Rydberg mixing. It must be remembered, however, that the performance of the MS-CASPT2 method relies on the previous mixing of the wave functions, and therefore it will not be unusual, depending on the employed basis set, to obtain CASPT2 results that already give the same answer as MS-CASPT2 results when the initial basis sets are changed.
10.5.3 Other cases.
The calculations become increasingly difficult with increased size of the system or in low symmetry cases. Common problems one has to solve are the selection of the active space when it is not possible to include all orbitals expected to be important and the presence of artificial valence-Rydberg mixing in the description of the states. Specific problems appear in systems containing transition metals, where there are a large amount of states close in energy.
To include all the required orbitals into the active space is sometimes
impossible. This is one of the important limitations of the methodology.
But some solutions are
available if one is aware of the limitations. References
[268] and [269] report
studies on the porphin and indigo molecules, respectively.
Porphin and indigo have 24 and 20 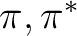 orbitals, respectively.
It is obviously impossible to include all of them in the active
spaces. The analysis of the configurations and occupation numbers
of the orbitals in a restricted number of excited states by means of
the RASSCF method has been found to be a useful procedure to
find a proper active space to study different states of the systems.
The RASSCF method is able to deal with a larger number of configurations
making possible to include all the
orbitals, respectively.
It is obviously impossible to include all of them in the active
spaces. The analysis of the configurations and occupation numbers
of the orbitals in a restricted number of excited states by means of
the RASSCF method has been found to be a useful procedure to
find a proper active space to study different states of the systems.
The RASSCF method is able to deal with a larger number of configurations
making possible to include all the 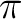 orbitals in the active space
and analyze the role of the different orbitals. Our goal in this case
is to be able to discard some of the deepest or highest orbitals if they
become less important in the description of the desired states.
orbitals in the active space
and analyze the role of the different orbitals. Our goal in this case
is to be able to discard some of the deepest or highest orbitals if they
become less important in the description of the desired states.
One possibility is to perform a SDTQ calculation involving all the presumably important active space (occupied orbitals in RAS1, empty orbitals in RAS3, no orbitals in RAS2, and four holes/electrons allowed in RAS1/RAS3). The occupation numbers for the active orbitals obtained for such calculation are usually similar to those of a full CASSCF treatment. Another possibility is to place in the CAS space (RAS2) the most important orbitals and the corresponding electrons and only allow singles and doubles excitations from RAS1 (occupied orbitals) to RAS3 (empty orbitals). In all these cases we will study the configurations and occupation numbers of the orbitals to find if some of them are or minor importance for the description of the states we are considering and then reduce the active space for the CASSCF/CASPT2 calculation [268,269].
Calculation on the excited states of transition metal compounds have to deal with another set of problems. For instance, the known 3d double-shell effect: two sets of d orbitals (3d and 4d) must be included in the reference space in order to obtain accurate results [26] in molecules containing metal atoms of the first transition row with many d-electrons (Fe-Zn). This is a severe limitation when more ligands are included together with the metal atom. Illustrations of such problems are the calculation of the cyanide and carbonyl transition metal compounds [26,270] and metal-protein models [271]. Core-valence [272] and relativistic effects [31] have been shown to be important for obtaining accurate results. Finally, the problem of the high multiplicity states in the standard CASPT2 formulation has to be considered. The zeroth-order Hamiltonian is defined as a Fock-type one-electron operator. Apart from the originally proposed Fock matrix [21,22], a correction, denoted g1 [29], has been designed so that CASSCF wave functions dominated by a closed-shell configuration, on the one hand, and an open-shell configuration, on the other hand, are treated in similar and balanced ways in the perturbation calculation. This correction was shown to be essential in order to obtain reliable results for the Cr2 molecule with the CASSCF/CASPT2 method [30].
Each type of system and situation has its own specific problems. Size and convergence problems in systems without any symmetry [273,274], symmetry breaking and localization problems in high symmetry cases [275], excited states in radical cations [276] and anions [277], etc. In addition, there are situations such as the crossing regions which require the simultaneous treatment of more than one state at the CASPT2 level, which can only be solved using the multi-state option in CASPT2.
Next: 10.6 Solvent models. Up: 10. Examples Previous: 10.4 High quality wave functions


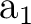 n orbital.
That is, our minimal valence active space can be labeled
(1302), where each number corresponds to the number of
n orbital.
That is, our minimal valence active space can be labeled
(1302), where each number corresponds to the number of 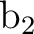 , and
, and